Что такое ПЛИС и как она работает
Параграфы "Цифровые схемы и логические вентили" и "Таблицы подстановки" во многом используют материалы статьи "How Does an FPGA Work?[1]" за авторством
Alchitry, Ell C, распространяемой по лицензии CC BY-SA 4.0.
История появления ПЛИС
До появления интегральных схем электронные устройства строились на базе вакуумных ламп, которые выполняли функции усиления и переключения. Эти лампы были громоздкими, энергозатратными и недолговечными. Затем их заменили на транзисторы, которые стали основой современных электронных схем. Поначалу транзисторы, как и лампы, использовались в виде отдельных компонентов, и схемы собирались из них, как модель из кубиков Lego. В случае ошибки её можно было исправить ручной корректировкой соединений между элементами, подобно исправлению ошибки при сборке модели Lego.
С развитием технологий произошла миниатюризация транзисторов, что позволило разместить их вместе с соединениями на одном кристалле. Так появились интегральные схемы — электронные схемы, выполненные на полупроводниковой подложке и заключённые в неразборный корпус. Этот переход стал революционным шагом в развитии электроники, открыв путь к созданию компактных и производительных устройств.
В большинстве случаев, исправить ошибку, допущенную при разработке и изготовлении интегральной схемы, невозможно. С учетом того, что изготовление прототипа интегральной схемы является долгим и затратным мероприятием (от десятков тысяч до миллионов долларов), возникла необходимость в гибком, быстром и дешёвом способе изготовления прототипа, и проверки на нём схемы до её изготовления. Так появились программируемые логические интегральные схемы (ПЛИС). В связи с повсеместным использованием англоязычной литературы, имеет смысл дать и англоязычное название этого класса устройств: programmable logic devices (PLD).
Стоит оговориться, что в данной книге под термином ПЛИС будет подразумеваться конкретный тип программируемых схем: FPGA (field-programmable gate array, программируемая пользователем вентильная матрица, ППВМ).
ПЛИС содержит некоторое конечное множество базовых блоков (примитивов), блоки межсоединений примитивов и блоки ввода-вывода. Подав определенный набор воздействий на ПЛИС (запрограммировав её), можно настроить примитивы, их межсоединения между собой и блоками ввода-вывода, чтобы получить требуемую цифровую схему. Удобство ПЛИС заключается в том, что в случае обнаружения ошибки на прототипе, исполненном в ПЛИС, вы можете исправить свою цифровую схему и повторно запрограммировать ПЛИС.
Кроме того, эффективно использовать ПЛИС не как средство дешевого прототипирования, но и как средство реализации конечного продукта в случае малого тиража (дешевле купить и запрограммировать готовую партию ПЛИС, чем изготовить партию собственных микросхем).
Давайте разберемся, что же это за устройство и как оно работает изнутри, но перед этим необходимо провести ликбез по цифровым схемам и логическим вентилям.
Цифровые схемы и логические вентили
Цифровые схемы
Цифровая схема — это абстрактная модель вычислений, которая оперирует двумя дискретными состояниями, обычно обозначаемыми как 0 и 1. Важно понимать, что эти состояния не привязаны к конкретным физическим величинам, таким как напряжение в электрической цепи. Вместо этого они представляют собой обобщенные логические значения, которые могут быть реализованы на любой технологии, способной различать два дискретных состояния.
Благодаря этой абстракции цифровые схемы могут быть реализованы не только с помощью традиционных электронных компонентов, но и на совершенно иных платформах, например на пневматических системах, из картона и шариков, красной пыли в игре Майнкрафт или даже с использованием человеческого взаимодействия, подобно тому, как это описано в романе Лю Цысиня "Задача трёх тел" (эффективность подобных схем — это уже другой вопрос). Основная идея заключается в том, что цифровая схема отвязывается от физической реализации, фокусируясь лишь на логике взаимодействия состояний 0 и 1, что делает её универсальной и независимой от конкретной технологии.
Разумеется, при проектировании эффективных цифровых схем необходимо оглядываться на технологию, по которой эти схемы будут работать.
В электронике словом "цифровая" описывают схемы, которые абстрагируются от непрерывных (аналоговых) значений напряжений, вместо этого используются только два дискретных значения: 0 и 1. На данном уровне абстракции нас не интересуют конкретные значения напряжений и пороги этих значений, что позволяет нам разрабатывать схему в идеальном мире, где у напряжения может быть всего два значения: 0 и 1. А обеспечением этих условий будут заниматься базовые блоки, из которых мы будем строить цифровые схемы.
Эти базовые блоки называются логическими вентилями.
Логические вентили
Существует множество логических вентилей, мы рассмотрим четыре из них: И, ИЛИ, Исключающее ИЛИ, НЕ. Каждый из этих элементов принимает на вход цифровое значение (см. цифровая схема), выполняет определенную логическую функцию над входами и подает на выход результат этой функции в виде цифрового значения.
Логические вентили на рис. 1-4 иллюстрируются условными графическими обозначениями (УГО), взятыми из двух стандартов: ANSI и ГОСТ. Ввиду повсеместного использования в литературе первого варианта, в дальнейшем в книге будет использован он.
Логический вентиль И принимает два входа и выдает на выход значение 1 только в том случае, если оба входа равны 1. Если хотя бы один из входов 0, то на выходе будет 0. На схемах логический вентиль И отображается следующим образом:
Рисунок 1. УГО логического вентиля И.
Логический вентиль ИЛИ принимает два входа и выдает на выход значение 1 в случае, если хотя бы один из входов равен 1. Если оба входа равны 0, то на выходе будет 0. На схемах логический вентиль ИЛИ отображается следующим образом:
Рисунок 2. УГО логического вентиля ИЛИ.
Логический вентиль Исключающее ИЛИ принимает два входа и выдает на выход значение 1 в случае, если значения входов не равны между собой (один из них равен 1, а другой 0). Если значения входов равны между собой (оба равны 0 или оба равны 1), то на выходе будет 0. На схемах логический вентиль Исключающее ИЛИ отображается следующим образом:
Рисунок 3. УГО логического вентиля Исключающее ИЛИ.
Логический вентиль НЕ — самый простой. Он принимает один вход и подает на выход его инверсию. Если на вход пришло значение 0, то на выходе будет 1, если на вход пришло значение 1, то на выходе будет 0. Он обозначается на схемах следующим образом:
Рисунок 4. УГО логического вентиля НЕ.
Также существуют вариации базовых вентилей, такие как И-НЕ, ИЛИ-НЕ, Исключающее ИЛИ-НЕ, отличающиеся от исходных тем, что результат операции инвертирован относительно результата аналогичной операции без -НЕ.
Логические вентили строятся из транзисторов. Транзистор — это элемент, который может пропускать/блокировать ток в зависимости от поданного напряжения на его управляющий вход.
Особенностью современных интегральных схем является то, что они строятся на основе комплементарной (взаимодополняющей) пары транзисторов P и N-типа (Комплементарная Металл-Оксид-Полупроводниковая, КМОП логика). Для данного типа транзисторов оказалось эффективнее реализовать операции И-НЕ и ИЛИ-НЕ.
С точки зрения построения цифровых схем МОП-транзисторы (P- и N-типа) можно воспринимать как выключатели, которые замыкают или размыкают связь между двумя выводами. Разница между P- и N типами заключается в значении напряжения на управляющем входе, при котором транзистор "открыт" (вход и выход замкнуты) или "закрыт" (связь разорвана). Рис. 5 иллюстрирует данное различие.
Выводы, между которыми образуется связь называются "сток" (drain, d) и "исток" (source, s), а управляющий вход — "затвор" (gate, g). Обратите внимание, что логический вентиль (logic gate) и затвор транзистора (просто gate) — это разные сущности!
Рисунок 5. МОП-транзисторы P и N типа.
На рис. 6 показан способ построения логических вентилей И-НЕ, ИЛИ-НЕ по КМОП технологии. Рассмотрим принцип работы вентиля И-НЕ.
Подача значения 1 на вход А или B открывает соответствующий этому входу n-канальный транзистор (обозначен на рис. 6 красным цветом) и закрывает дополняющий его (комплементарный ему) p-канальный транзистор (обозначен синим цветом). Подача на оба входа 1 закрывает оба p-канальных транзистора (верхняя часть схемы разомкнута, что для значения на выходе означает, что её будто и нет) и открывает оба n-канальных транзистора. В результате чего выход замыкается на "землю" (чёрный треугольник внизу схемы), что эквивалентно 0 в контексте цифровых значений.
В случае, если хотя бы на одном из входов А или B будет значение 0, откроется один из параллельно соединенных p-канальных транзисторов (в то время как соединение с "землей" будет разорвано) и выход будет подключен к питанию (две перпендикулярные линии вверху схемы), что эквивалентно 1 в контексте цифровых значений.
Как вы видите, напряжение на выход подается от источников постоянного питания или земли, а не от входов вентиля, именно этим и обеспечивается постоянное обновление напряжения и устойчивость цифровых схем к помехам.
Рисунок 6. Схема логических вентилей И-НЕ, ИЛИ-НЕ, построенных на КМОП транзисторах.
Как правило, при необходимости инвертировать вход или выход логического элемента на схеме, на нем рисуют кружок вместо добавления логического вентиля НЕ в том виде, котором он изображён на рис. 4. К примеру, логический элемент И-НЕ обозначают в виде, представленном на рис. 6.
При желании, из логического элемента И-НЕ можно легко получить логический элемент И (как и элемент ИЛИ из ИЛИ-НЕ). Для этого необходимо поставить на выходе И-НЕ инвертор, собираемый из двух МОП-транзисторов по схеме, представленной на рис. 7.
Рисунок 7. Схема логического вентиля НЕ, построенного на КМОП транзисторах.
КМОП логика далеко не единственный способ построения цифровых элементов, ранее достаточно широко применялись другие варианты построения схем, например только на одном типе транзисторов. Однако наиболее эффективным оказалось использование именно комплементарных пар, и на сегодня такой подход для цифровых схем является доминирующим.
Используя одни лишь описанные выше логические вентили можно построить любую(!) цифровую схему.
Однако, при описании цифровых схем, некоторые цифровые блоки используются настолько часто, что для них ввели отдельные обозначения (сумматоры, умножители, мультиплексоры т.п.), используемые при описании более сложных схем. Рассмотрим один из фундаментальных строительных блоков в ПЛИС — мультиплексор.
Мультиплексоры
Мультиплексор — это устройство, которое в зависимости от значения управляющего сигнала подает на выход значение одного из входных сигналов.
УГО мультиплексора представлено на рисунке 8.
Рисунок 8. Обозначение Мультиплексора.
Символ / на линии sel указывает на то, что данный сигнал является многоразрядным, а число ниже указывает на то, что разрядность сигнала составляет 6 бит.
Число входов мультиплексора может быть различным, но выход у него всегда один.
Способ, которым кодируется значение управляющего сигнала может также различаться. Простейшая цифровая схема мультиплексора получится, если использовать унитарное (one-hot) кодирование. При таком кодировании, значение многоразрядного управляющего сигнала всегда содержит ровно одну 1. Информация, которую несёт закодированный таким образом сигнал содержится в положении этой 1 внутри управляющего сигнала.
Посмотрим, как можно реализовать мультиплексор с управляющим сигналом, использующим one-hot-кодирование, при помощи одних лишь логических вентилей И, ИЛИ:
Рисунок 9. Реализация мультиплексора, использующего one-hot кодирование.
Если мы выставим значение управляющего сигнала, равное 000010, означающее, что только первый бит этого сигнала (счет ведется с нуля) будет равен единице (sel[1] = 1), то увидим, что на один из входов каждого логического вентиля И будет подано значение 0. Исключением будет логический вентиль И для входа b, на вход которого будет подано значение 1. Это означает, что все логические вентили И (кроме первого, на который подается вход b) будут выдавать на выход 0 (см. Логические вентили) вне зависимости от того, что было подано на входы a,c,d,e и f. Единственным входом, который будет влиять на работу схемы, окажется вход b. Когда он равен 1, на выходе соответствующего логического вентиля И окажется значение 1. Когда он равен 0 на выходе И окажется значение 0. Иными словами, выход И будет повторять значение b.
Рисунок 10. Реализация мультиплексора, использующего one-hot кодирование.
Логический вентиль ИЛИ на данной схеме имеет больше двух входов. Подобный вентиль может быть создан в виде каскада логических вентилей ИЛИ:
Рисунок 11. Реализация многоходового логического ИЛИ.
Многовходовой вентиль ИЛИ ведет себя ровно так же, как двухвходовой: он выдает на выход значение 1, когда хотя бы один из входов равен 1. В случае, если все входы равны 0, на выход ИЛИ пойдет 0.
Для нашей схемы мультиплексора гарантируется, что каждый вход ИЛИ кроме одного будет равняться 0 (поскольку выход каждого И кроме одного будет равен 0). Это означает, что выход многовходового ИЛИ будет зависеть только от одного входа (в случае, когда sel = 000010 — от входа b).
Рисунок 12. Реализация мультиплексора, использующего one-hot кодирование.
Меняя значение sel, мы можем управлять тем, какой из входов мультиплексора будет идти на его выход.
Программируемая память
Из транзисторов можно построить не только логические элементы, но и элементы памяти. На рис. 13 представлена схема простейшей ячейки статической памяти, состоящей из транзистора и двух инверторов (т.е. суммарно состоящей из 5 транзисторов, поэтому она называется 5T SRAM). Данная ячейка реализует 1 бит программируемой памяти, являвшейся одним из основных компонентов самой первой ПЛИС.
Рисунок 13. Программируемая ячейка памяти ПЛИС Xilinx XC2064[2, стр. 2-63].
Данная память представляет собой бистабильную ячейку — петлю из двух инверторов, в которых "заперто" хранимое значение. Дважды инвертированный сигнал совпадает по значению с исходным, при этом, проходя через каждый из инверторов, сигнал обновляет свое значение напряжения, что не позволяет ему угаснуть из-за сопротивления цепи.
Для того чтобы поместить в бистабильную ячейку новое значение, к её входу подключается еще один транзистор, замыкающий или размыкающий её с напряжением питания/земли.
Таблицы подстановки (Look-Up Tables, LUTs)
Представьте мультиплексор с четырьмя входными сигналами и двухбитным управляющим сигналом (обратите внимание, что теперь это сигнал использует обычное двоичное кодирование). Но теперь, вместо того чтобы выставлять входные сигналы во внешний мир, давайте подключим их к программируемой памяти. Это означает, что мы можем "запрограммировать" каждый из входов на какое-то константное значение. Поместим то, что у нас получилось, в отдельный блок и вот, мы получили двухвходовую Таблицу подстановки (Look-Up Tables, далее LUT).
Рисунок 14. Реализация таблицы подстановки (Look-Up Table, LUT).
Эти два входа LUT являются битами управляющего сигнала мультиплексора, спрятанного внутри LUT. Программируя входы мультиплексора (точнее, программируя память, к которой подключены входы мультиплексора), мы можем реализовать на базе LUT любую(!) логическую функцию, принимающую два входа и возвращающую один выход.
Допустим, мы хотим получить логическое И. Для этого, нам потребуется записать в память следующее содержимое:
| Адрес ({x, y}) | Значение (f) |
|---|---|
| 00 | 0 |
| 01 | 0 |
| 10 | 0 |
| 11 | 1 |
Это простейший пример — обычно LUT-ы имеют больше входов, что позволяет им реализовывать более сложную логику.
D-триггеры
Как вы уже поняли, используя неограниченное количество LUT-ов, вы можете построить цифровую схему, реализующую логическую функцию любой сложности. Однако цифровые схемы не ограничиваются реализацией одних только логических функций (цифровые схемы, реализующие логическую функцию, называются комбинационными, поскольку выход зависит только от комбинации входов). Например, так не построить цифровую схему, реализующую процессор. Для таких схем нужны элементы памяти. Заметим, что речь идет не о программируемой памяти, задавая значения которой мы управляем тем, какие логические функции будут реализовывать LUT-ы. Речь идет о ячейках памяти, которые будут использоваться логикой самой схемы.
Такой базовой ячейкой памяти является D-триггер (D flip-flop). Из D-триггеров можно собирать другие ячейки памяти, например регистры (а из регистров можно собрать память с произвольным доступом (random access memory, RAM)), сдвиговые регистры и т.п.
D-триггер — это цифровой элемент, способный хранить один бит информации. В базовом варианте у этого элемента есть два входа и один выход. Один из входов подает значение, которое будет записано в D-триггер, второй вход управляет записью (обычно он называется clk или clock и подключается к тактирующему синхроимпульсу схемы). Когда управляющий сигнал меняет своё значение с 0 на 1 (либо с 1 на 0, зависит от схемы), в D-триггер записывается значение сигнала данных. Обычно, описывая D-триггер, говорится, что он строится из двух триггеров-защелок (D-latch), которые, в свою очередь, строятся из RS-триггеров. Однако в конечном итоге, все эти элементы могут быть построены на базе логических вентилей И/ИЛИ, НЕ:
Рисунок 15. Реализация D-триггера.
Арифметика
Помимо описанных выше блоков (мультиплексоров и построенных на их основе LUT-ов и регистров) выделяется еще один тип блоков, настолько часто используемый в цифровых схемах, что его заранее размещают в ПЛИС в больших количествах: это арифметические блоки. Эти блоки используются при сложении, вычитании, сравнении чисел, реализации счётчиков. В разных ПЛИС могут быть предустановлены разные блоки: где-то это может быть 1-битный сумматор, а где-то блок вычисления ускоренного переноса (carry-chain).
Все эти блоки могут быть реализованы через логические вентили, например так можно реализовать сумматор:
Рисунок 16. Реализация полного однобитного сумматора.
Логические блоки
В предыдущих параграфах, были рассмотрены отдельные виды цифровых блоков: таблицы подстановок, регистры, арифметические блоки. Для удобства структурирования, эти блоки объединены в ПЛИС в виде логических блоков. Обычно, логические блоки современных ПЛИС состоят из логических ячеек (или логических элементов), но для простоты повествования, мы объединим все эти термины.
Логический блок может содержать одну или несколько LUT, арифметический блок, и один или несколько D-триггеров, которые соединены между собой некоторым количеством мультиплексоров. На рисунке 17 представлена схема того, как может выглядеть логический блок:
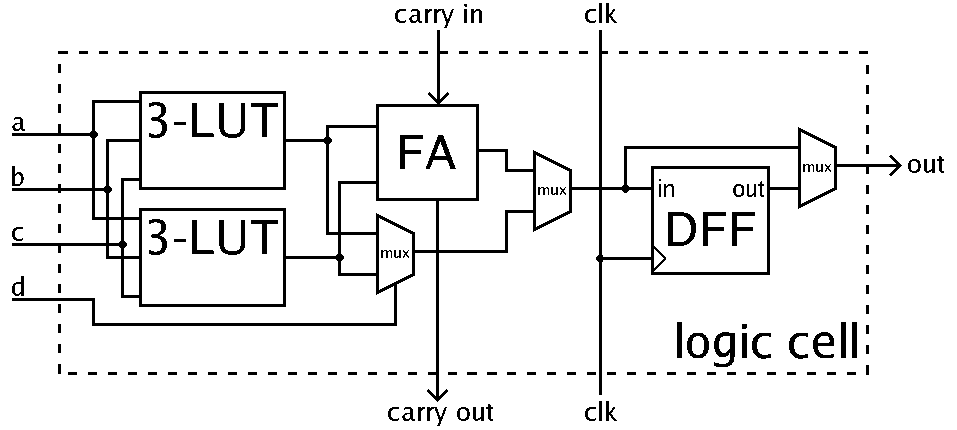
Рисунок 17. Схема логической ячейки[2].
Логический блок представляет собой цепочку операций: логическая функция, реализованная через LUT -> арифметическая операция -> Запись в D-триггер. Каждый из мультиплексоров определяет то, будет ли пропущен какой-либо из этих этапов.
Таким образом, конфигурируя логический блок, можно получить следующие вариации кусочка цифровой схемы:
- Комбинационная схема (логическая функция, реализованная в LUT)
- Арифметическая операция
- Запись данных в D-триггер
- Комбинационная схема с записью результата в D-триггер
- Арифметическая операция с записью результата в D-триггер
- Комбинационная схема с последующей арифметической операцией
- Комбинационная схема с последующей арифметической операцией и записью в D-триггер
На рисунке 18 приведён реальный пример использования логического блока в ПЛИС xc7a100tcsg324-1 при реализации Арифметико-логического устройства (АЛУ), подключенного к периферии отладочной платы Nexys-7. На этом рисунке вы можете увидеть использование LUT-ов, арифметического блока (ускоренного расчета переноса), и одного из D-триггеров. D-триггеры, обозначенные серым цветом, не используются.
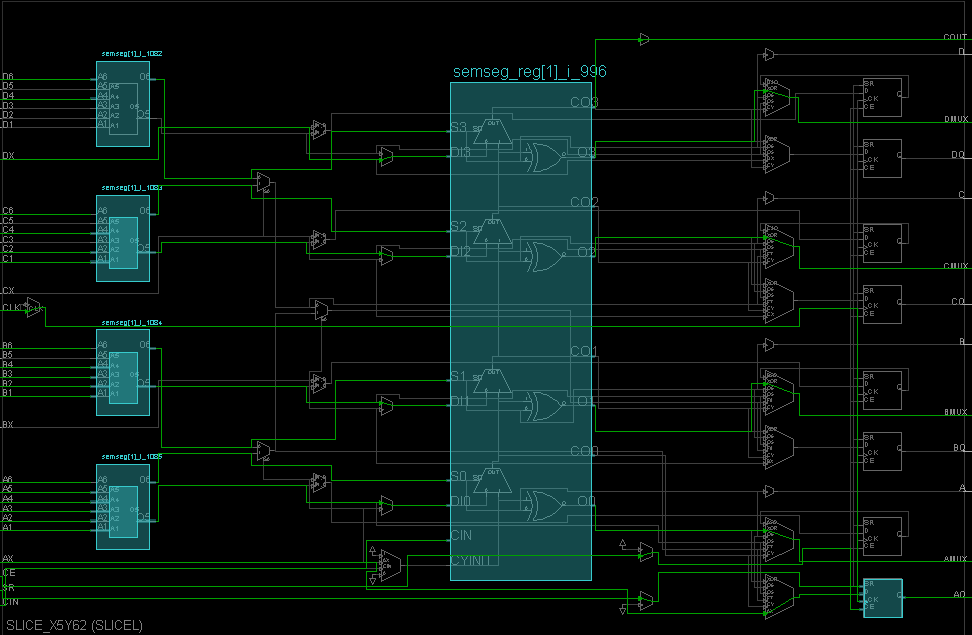
Рисунок 18. Пример использования логической ячейки.
Располагая большим наборов таких логических блоков, и имея возможность межсоединять их нужным вам образом, вы получаете широчайшие возможности по реализации практически любой цифровой схемы (ограничением является только ёмкость ПЛИС, т.е. количество подобных логических блоков, входов выходов и т.п.).
Помимо логических блоков в ПЛИС есть и другие примитивы: блочная память, блоки умножителей и т.п.
Сеть межсоединений
Для того чтобы разобраться, как управлять межсоединением логических блоков, рассмотрим рис. 19, входящий в патент на ПЛИС[4].
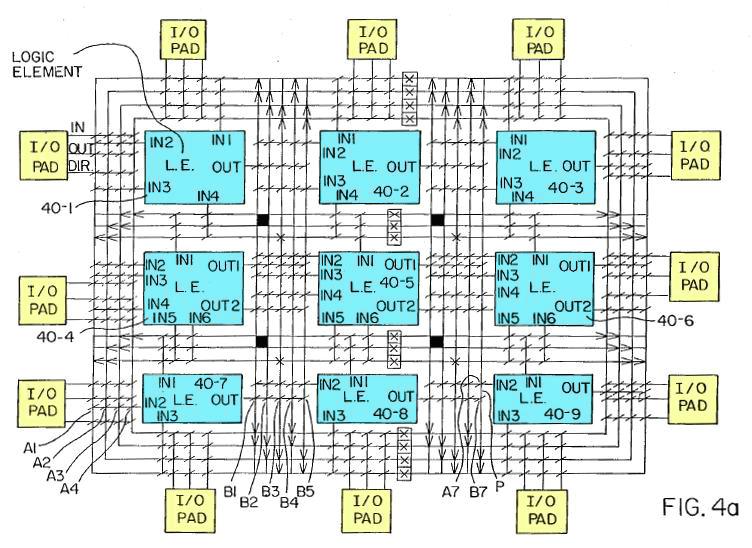
Рисунок 19. Содержимое ПЛИС в виде межсоединения логических блоков и блоков ввода-вывода[5].
Синим показано 9 логических блоков, желтым — 12 блоков ввода-вывода. Все эти блоки окружены сетью межсоединений (interconnect net), представляющей собой решётку из горизонтальных и вертикальных соединительных линий — межсоединений общего назначения (general purpose interconnect) [2, 2-66].
Косыми чертами в местах пересечения линий обозначены программируемые точки межсоединений (programmable interconnect points, PIPs), представляющие собой транзисторы, затвор которых подключен к программируемой памяти.
Управляя значением в подключенной к затвору транзистора памяти, можно управлять тем, что из себя будет представлять транзистор в данной точке: разрыв, или цепь. А значит, можно удалять "лишние" участки сети, оставляя только используемые логические блоки, соединенные между собой.
Итоги главы
- Используя такие элементы, как транзисторы, можно собирать логические вентили: элементы И, ИЛИ, НЕ и т.п.
- Используя логические вентили, можно создавать схемы, реализующие как логические функции (комбинационные схемы), так и сложную логику с памятью (последовательностные схемы).
- Из логических вентилей строится и такая важная комбинационная схема, как мультиплексор: цифровой блок, который в зависимости от значения управляющего сигнала подаёт на выход один из входных сигналов.
- Кроме того, подключив вход бистабильной ячейки (представляющую собой петлю из двух инверторов) к транзистору, можно получить 1 бит программируемой памяти.
- Подключив входные сигналы мультиплексора к программируемой памяти, можно получить Таблицу подстановок (Look-Up Table, LUT), которая может реализовывать простейшие логические функции. LUT-ы позволяют заменить логические вентили И/ИЛИ/НЕ, и удобны тем, что их можно динамически изменять. Логические вентили в свою очередь исполняются на заводе и уже не могут быть изменены после создания.
- Из логических вентилей также можно собрать базовую ячейку памяти: D-триггер, и такую комбинационную схему как полный 1-битный сумматор (или любой другой часто используемый арифметический блок).
- Объединив LUT, арифметический блок и D-триггер получается структура в ПЛИС, которая называется логический блок.
- Логический блок (а также другие примитивы, такие как блочная память или умножители) — это множество блоков, которые заранее физически размещаются в кристалле ПЛИС, их количество строго определено конкретной ПЛИС и не может быть изменено.
- Подключая программируемую память к транзисторам, расположенных в узлах сети межсоединений, можно управлять расположением разрывов в сети, а значит можно оставить только маршрут, по которому сигнал пойдет туда, куда нам нужно (трассировать сигнал).
- Конфигурируя примитивы и трассируя сигнал между ними (см. п.4), можно получить практически любую цифровую схему (с учетом ограничения ёмкости ПЛИС).
Список источников
- Alchitry, Ell C / How Does an FPGA Work?
- Xilinx / The Programmable Gate Array Data Book
- Wikipedia / Field-programmable gate array
- Ross H. Freeman / Configurable electrical circuit having configurable logic elements and configurable interconnects / United States Patent
- Ken Shirriff / Reverse-engineering the first FPGA chip, the XC2064